子どもに勉強を教えていますが、どのような教え方がいいのか迷います。あまり口出しすると喧嘩になってしまいます…。
テストの点数、通知表、塾の模試、等など、特に小学生になると、具体的な数値となりあらわれるため、気になってしまうお子様の成績。
幼児期や小学生低学年の間は、親御さんがお子様の勉強を教えたり、
高学年や中学生になってもお子様の成績を気にかけ、アドバイスする親御さんが多いのではないでしょうか。
勉強のアドバイスをするときや、具体的な内容を教えるときにも、役立つ学力向上の仕組みを説明します。
ぜひ、最後までお読みください(^^)
この記事を読んで分かること
・学力が向上するプロセス「①理解→②定着→③活用」を説明
・学力向上のイメージをより具体に膨らませることができる
・お子様の指導の参考にして頂けれると幸いです。
子どもことは、なんだって心配なのが親心というものでしょうか…。
学力向上のプロセス
勉強はやみくもにやっても、成績は上がりません。
小学3年生の子に、習ってもいない小学6年生の問題集を何ページもやらせても、身につきません。
極端な例ですが、なんとなくイメージがつくのではないでしょうか。
学力は「①理解→②定着→③活用」の3段階を経て向上していきます。
上記のプロセスに乗っかり勉強すれば、必ず成績は向上します。
「理解、定着、活用」と言われても、なかなか具体的なイメージがつきにくいかと思いますので、具体的な問題を参考にしながら、手順を解説していきます。
まずは、以下の問題をご覧ください。
問題:以下の図の赤い部分の面積を求めなさい。円周率は3.14とする。
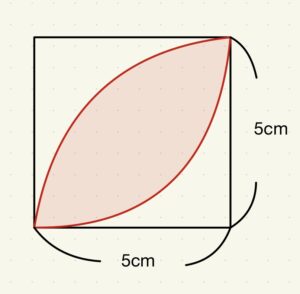
小学5年生の問題です。よく見るタイプの問題です。
では、この問題を解くためにはどのような手順で正解に辿りつけばいいのかを説明していきます。
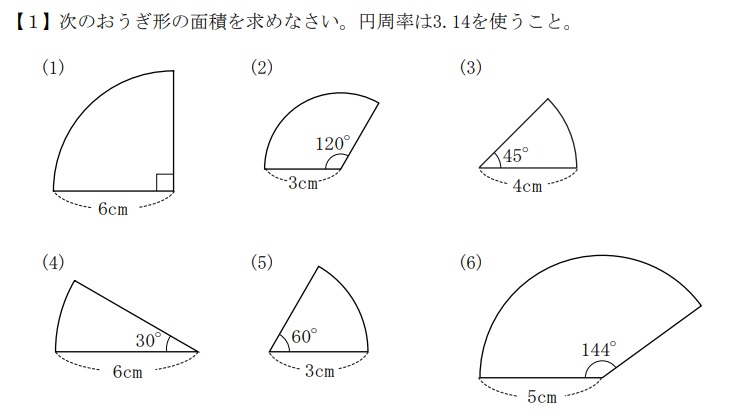
①理解:単元の概要や知識の把握
ここでいう理解とは、単元の概要を把握したり、基本的な知識を理解することです。
先ほどの問題を解くためには以下の4つの知識が必要となります。
・円の面積を求める公式
・おうぎ形の面積を求める公式
・三角形の面積を求める公式
・小数点のある計算
問題を解く上で最低限必要な知識を暗記している状態が「理解」となります。
公式であれば、公式の意味や使い方、社会や理科の用語であれば重要語句や語句の意味です。
学校や塾の授業が「理解」にあたります。
まずは、単元の概要理解を深め、基礎知識の習得をします。
しかし、基礎知識を習得しただけでは、テストで点数は取れません。
問題演習を行い、知識の定着を行うことに繋げます。
②定着:理解で得た知識を使い基礎問題の演習
「理解」ができたら、「理解」の領域で得た知識を使い基礎問題の演習をしていきます。
このような問題です。よく問題集でも見る出題形式です。
公式に具体的な数字を当てはめ解答します。
公式は正しく覚えられているか、計算のルールを正しく理解できているか、計算ミスをしていないか、などを確認できる領域となります。
正確性・問題処理スピードを鍛えます。
先ほどの問題では、以下の3点を求められれば正解にたどり着きます。
①半径5センチの円の面積を求める
②中心角90度のおうぎ形の面積を求める。
③底辺・高さ5センチの直角二等辺三角形の面積を求める。
この問題の場合、円・おうぎ形・三角形の公式を使いこなせるようになっても、
円周率が「3.14」という複雑な数字となるため、計算ミスが起こりやすいです。
また、おうぎ形を求めるにはわり算や分数を使い計算するため、上記(6)のように中心角144度などの細かい数値だと、さらに計算ミスを起こす可能性が高くなります。
どの問題を解いても、計算ミスなく、スピーディーに問題をこなせる能力が必要となります。
注意点として、定着の領域を極めただけでは学力向上はしません。
なぜなら、「基礎問題、完璧に解けます✌️」という状態になっても、
実際の入試問題が解けたり、入試での合格基準の学力に到達できる可能性は低いからです。
定着の領域をある程度網羅できたら、次は「③活用」の単元に入っていきます。
③活用:基礎知識を活かし、難易度高めな応用問題の演習
公式や基礎知識を習得し、基礎問題を解けるようになった次は、応用問題の演習です。
経験がある人はなんとなく分かると思いますが、中・高・大学の入試問題は半分以上応用問題です。
志望進路に進むために勉強している人がほとんどだと思います。
そのため、応用問題を解けるようになることは必須です。
先ほどの問題を例にすると、正方形の対角線上に補助線を引くと分かりやすくなります。
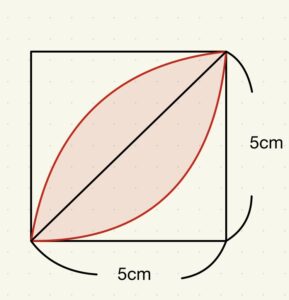
こんな感じです。
①中心角が90度のおうぎ形から三角形を引く。
②赤い部分の上側の面積が求めらる。
③②が二つ分あるため、×2をする。
上記のように解けば、答えにたどり着きます。
式にするとこんな感じです。
①5×5×3.14÷4=19.625(おうぎ形の面積)
5×5÷2=12.5(三角形の面積)
②19.625-12.5=7.125(赤い上の部分)
③7.125×2=14.25
答え:14.25㎠
といった感じで答えを出すことができます。
演習の領域では公式を使うだけではなく、
公式を使い問われている図形を求めるにはどのような道筋を進めばいいか、
論理を組み立て立式することが重要となります。
簡単に言うと、応用問題となるため、入試問題や学校のテストで高得点を取得したい場合は重要な領域となります。
しかし、いきなり応用問題を解くことは難しいため、「①理解」「②定着」の訓練も併せて重要になるということです。
理解・定着・活用の位置づけ
学力向上のプロセス、なんとなく理解できたでしょうか?
お子様の成績が伸び悩み、アドバイスをするのであれば、どこでつまずいているのかを確認し、
基礎問題の演習が足りていなければ、定着の領域を習得できる問題演習を、
基礎問題は正解できるが、応用問題の正答率が低いのであれば、
応用問題の解説を見ながら解法パターンを習得するようにアドバイスするのが適切だと考えます。
理解の領域は、学校や塾の「授業」で学ぶことです。
定着・活用の領域は、「自主学習」です。
学校や塾の授業だけを聞いて「分かった!」と納得しても、なかなかテストの点数は取れません。
特に学年が上がれば上がるにつれ、実感しやすくなるのではないでしょうか。
定着・活用の「自学」の時間を十分に確保することで学力は向上します。
自主学習するときは、集中力を最大限に生かし勉強しましょう。
まとめ
以上が、学力向上のプロセスでした。
よく「正しい努力をしないと結果が出ない」というようなことを言われますが、
勉強でも同じことが言えます。
子どもは、今自分がどこでつまずいているのか理解しにくいことがあるため、
大人が正しい努力の方法を導けるよう、子どもをよく観察し見守り指導していきたいと考えています。













