苦手単元を克服するのはいつがいい!?
幼児期頃から勉強を始め、ある程度の難易度まで辿り着くと出てくる悩みは「苦手単元の克服のタイミング」に関してです。
◯◯の単元が苦手なので、たくさん宿題を出してください!
と、よく親御さんからお願いされることが多々あります。
受験期であれば、苦手単元の克服が合否の鍵になることもありますが、
幼児期・小学校低学年や、勉強を本格的にし始めたばかりの子は、苦手単元ではなく、まずは得意単元を伸ばすことに特化した方がいいです。
勉強していれば、いずれ苦手単元にぶつかりますが、得意単元を伸ばしておくことで乗り越え方の負担が少なくてすみます。
本日は、具体事例をもとに、まずは得意単元を伸ばすことに注力した方がいい理由を紹介していきます。
得意を伸ばした方がいい理由
難易度の低い問題の大量の演習が、難易度の高い問題の正答率に繋がる
一般的に苦手単元となるは、難易度の高い単元です。
好き嫌いは別で、「計算の単元は苦手で、図形の単元は得意です!」と言う生徒は少数派です。
特に算数・数学は積み重ねの科目のため、得意である難易度を落とした問題を数多く演習すれば、苦手単元を克服できるきっかけになることは往々にしてあります。
例えば、「2ケタ+2ケタの繰り上がりの足し算」の単元が苦手な子がいたとします。
宿題やテストで、正答率が上がらず、解くことさえも困難だとします。
その子に「2ケタ+2ケタの繰り上がりの足し算」が苦手だからといって、
毎日「2ケタ+2ケタの繰り上がりの足し算」を課題として出し、そればかりさせ続けたらどうなるでしょう!?
きっと勉強が嫌いになり、勉強から距離を置いてしまいます。
そもそも上記の対策では「2ケタ+2ケタの繰り上がりの足し算」はできるようになりません。
「2ケタ+2ケタ」の足し算の正答率が低く、理解度が低い場合は、どの工程から苦手になったのかを確認すべきです。
- 繰り上がりなし1ケタ+1ケタ 例)3+3=6
- 繰り上がりなし2ケタ+1ケタ 例)12+5=17
- 繰り上がりあり1ケタ+1ケタ 例)8+6=14
- 繰り上がりあり2ケタ+1ケタ 例)16+7=23
- 繰り上がりなし2ケタ+2ケタ 例)12+14=26
以上のどの部分でつまづいているかを確認します。
つまづいているかの確認方法は、100問ほど解いてミスがなく一人で解ければ完全に理解しているということです。
100問解くのが1日で終わさなくても、何日間に分けても大丈夫です。
100問と聞くと多いと感じるかもしれませんが、ケアレスミスをしているようでは、完全に理解したとは言えません。
つまづいている単元は、自力で解くことはできるが、明らかにペースが遅かったり、ミスを連発するため、保護者はすぐに気が付くと思います。
先ほどの「2ケタ+2ケタの繰り上がりの足し算」の単元が苦手な子が、
③繰り上がりあり1ケタ+1ケタで、解くスピードが落ちる、ミスが極端に増える等の異変を感じたら、
その子の苦手は繰り上がりありの1ケタ+1ケタから重点的に勉強を始めるのがいいです。
自力では解けるため、あとは慣れるだけ!
ということなので、「2ケタ+2ケタの繰り上がりの足し算」を解くことより、だいぶハードルが下がります。
上記③から始め、④→⑤と難易度を上げていき、③④⑤がスラスラと解けるようになった後、「2ケタ+2ケタの繰り上がりの足し算」を解いてみてください。
きっと、できるようになっていますよ(^^)
計算力を高める方法は、以下の記事でも紹介しています。ぜひ参考にしてください。
自信がついて、苦手に挑戦できるようになる
これは想像しやすいのではないでしょうか。
例えば、算数では「計算得意!」という子は多いです。
計算分野は、比較的、難易度の低い分野だからです。
取り組みやすい計算を100マス計算のタイムを縮めるために、計算問題を毎日100問以上解く等計算分野を極めたとします。
それだけたくさんの計算をしていたら、学校の小テストやカラーテストで良い結果が出てきます。
当たり前ですが、良い結果が出てくると、自信がつきます。先生や親御さんに褒められて嬉しくなることもあるでしょう。
子どもだけでなく、大人も自信がついた分野は、前向きに取り組めるようになります。
計算ができたら、次は文章問題も勉強してみようか、図形問題も、と次々と難しい単元でも取り組んでみようというチャレンジ精神が湧いてきます。
子どものチャレンジ精神が湧いてくれば、親御さんは日々の勉強の進捗確認&応援をすればいいだけなので、精神的にも楽になります。
基礎知識が複数合わさったものが応用問題となる
長い文章で出題される応用問題は難しい!と思われがちですが、応用問題の多くは基礎知識を複数組み合わせれば解ける問題がほとんどです。
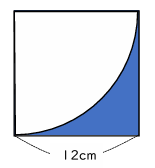
例えば、上記問題は「色のついた部分の面積を求めましょう」という、小学6年生で学習する「円」の単元の問題です。
パッと見ると、こんなヘンテコな形、求めるなんて難しいと思うかもしれません。
この問題を解く工程は以下の通りです。
- 白い図形は円の4分の1である扇形であることに気付く。
- 大きな正方形の面積を求める。
- 半径12センチの円を求める。
- ③で求めた円の4分の1の扇形を求める。
- ②の正方形から④の扇形をひく。
こうすると解答まで辿り着きます。
小学生の問題にしては、工程が多く、自力で正解までたどり着くのは難しいです。
また、1辺が12センチということで、数が大きい計算になり、計算ミスも増えそうな問題です。
しかし、一工程ずつ問題になっていたらどうでしょうか!?
例えば、「1辺が12センチの正方形の面積を求めなさい」(上記②の工程)と単独で問題が出題されれば、一気に正答率は上がります。
正方形の面積は、小学校4年生で習う単元ですからね。
「半径12センチの円の面積を求めなさい」(上記③の工程)という単独の問題でも同じです。
このように、応用問題は基礎知識の組み合わせでできています。
一工程ずつの問題であれば正解できるのに、
応用問題となれば多くの工程があり、さらにそれらの工程の順番を自分で考え立式し、答えを出す、という多くの思考が必要となります。
応用問題を解くためには、基礎知識の演習を増やし、公式の使い方、正確に計算する能力を身に付ける必要があります。
あとは、論理的思考や立式等を訓練するだけです。
前述の通り、基礎問題は得意、応用問題は苦手、となる生徒が多いため、得意の基礎問題を極めると応用問題も解けやすくなります。
まとめ:苦手は得意を伸ばしきってから!
苦手単元があると親も子も焦るものです。
「この単元の勉強したくないなぁ~」とどうしても後ろ向きになってしまいます。
勉強は、避けようと思えばいくらでも避けてれてしまうため、できるだけ前向きな姿勢で取り組むことをお勧めします。
そのためには、最初は「とにかく得意を極める」ことを念頭に置いて勉強しましょう。
基礎的な計算でも、漢字でも、なんでもいいのです。
上述の通り、難しい応用問題でも多くが基礎知識の組み合わせです。
基礎ができていてこそ、難しい応用問題に取り組めるのです。
何か一つでも参考になれば嬉しいです!















